1の16乗根が作る累巡回拡大体を図示する

ℚ(ζ)/ℚとその拡大次数

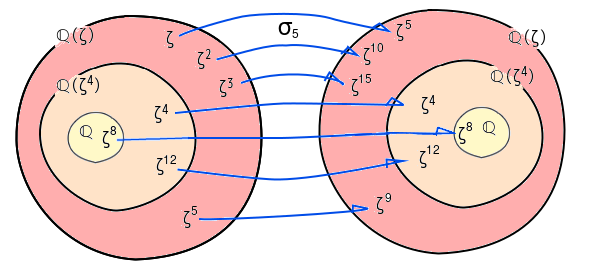
前提条件を繰り返しておきます。

x¹⁶-1=0 の解は ζ = cos(360˚/16)+isin(360˚/16) として、1,ζ,ζ²,ζ³,…,ζ¹⁵の16個です。

ζのℚ上の最小多項式は16次の円分多項式、Φ₁₆(x)=O で、その根は ζ,ζ³,ζ⁵,ζ⁷,ζ⁹,…,ζ¹⁵ と2の倍数を除いたもので8個です。

ガロア群Gal(ℚ(ζ)/ℚ)の元は、ℚ(ζ)のζⁱを別のζ^jに対応付ける写像のうち、1の原始16乗根に移すものになります。

その元を、

σi(ζ)=ζi (i=1,3,5,7,…,15)

とします。σ₁は恒等変換です。

ℚ(ζ)/ℚの拡大次数8、ガロア群Gal(ℚ(ζ)/ℚ)の位数も8です。

ℚ(ζ)/ℚ(ζ^4)の自己同型写像の図示法を工夫する

前にσ₅の作用を図示しました。

これをプログラムで作成できるように、次のように書き換えてみます。上下の対応を確認してください。

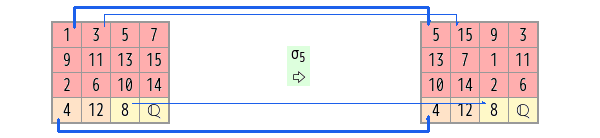
表の各セルを各ζⁱに対応させて、その指数だけを書くことにします。

最後の1行がℚ(ζ⁴), あるいはℚの範囲です。

上部3行はℚ(ζ)ですが、偶数乗は奇数乗と異なる変換のされ方をするので分けてあります。

こうしておくと固定される部分の ℚ(ζ⁴)/ℚの自己同型写像を縦に書くことができます。

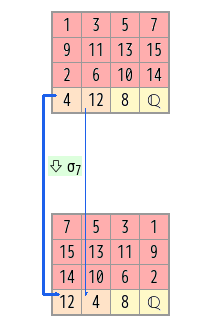
この変換は ℚ(ζ⁴) の範囲だけでいいような気もしますが、ℚ(ζ) 全体でもうまく回ってるので表示しています。

この表を作成したプログラムは、「mod 16」で紹介しています。タイトルやメニューはまだ仮です。

・<σ5>と<σ7>による2段階の累巡回の図示

まず、<σ₅>と<σ₇>で考えます。

Gal(ℚ(ζ)/ℚ(ζ4)) = <σ5> = {e, σ5, σ9, σ13}
Gal(ℚ(ζ4)/ℚ) = <σ7> = {e,σ7}

σ₅を複数回作用させると4回目にもとに戻ります。

2回作用させるとσ₉、3回作用させるとσ₁₃、4回作用させるとσ₁=e と同等であることもわかります。

⇩ σ₇ を作用させると、固定体であった部分が変換されます。

そこから σ₅を複数回作用させると別の経路で巡回し、4回目にもとに戻ります。

⇩ σ₇　さらに作用させると、もとに戻ります。

これで、σ_i(ζ)=ζⁱ (i=1,3,5,7,…,15) の写像の全部が出現しています(表の1-1のセルでわかります)。

・立体図にしてみる

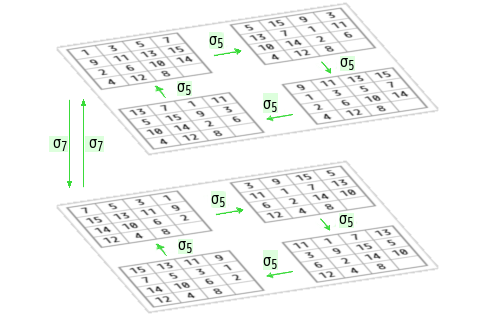
巡回のイメージをつかむために、このように見てください。第一層(上の層)では1-5-9-13しか回りませんが、σ₇によって1が第二層に降りると7-3-11-15と回って全部の写像が出てきます。1-7だけでなく、5-3など上下に並んでいるものはどれもσ₇で相互に変換されます。

・<σ5>と<σ15>による2段階の累巡回の図示

2つ目、<σ₅>と<σ₁₅>で考えます。

Gal(ℚ(ζ)/ℚ(ζ4)) = <σ5> = {e, σ5, σ9, σ13}
Gal(ℚ(ζ4)/ℚ) = <σ15> = {e,σ15}

⇩ σ₁₅ を作用させると、固定体であった部分が変換されます。

そこから σ₅を複数回作用させると別の経路で巡回し、4回目にもとに戻ります。

σ₁₅ をさらに作用させると、もとに戻ります。

・<σ13>と<σ7>による2段階の累巡回の図示

3つ目、<σ₁₃>と<σ₇>で考えます。

Gal(ℚ(ζ)/ℚ(ζ4)) = <σ13> = {e, σ13, σ9, σ5}
Gal(ℚ(ζ4)/ℚ) = <σ7> = {e,σ7}

⇩ σ₇ を作用させると、固定体であった部分が変換されます。

そこから σ₁₃を複数回作用させると別の経路で巡回し、4回目にもとに戻ります。

σ₇ をさらに作用させると、もとに戻ります。

・<σ13>と<σ15>による2段階の累巡回の図示

4つ目、<σ₁₃>と<σ₁₅>で考えます。

Gal(ℚ(ζ)/ℚ(ζ4)) = <σ13> = {e, σ13, σ9, σ5}
Gal(ℚ(ζ4)/ℚ) = <σ15> = {e,σ15}

⇩ σ₁₅ を作用させると、固定体であった部分が変換されます。

そこから σ₁₃を複数回作用させると別の経路で巡回し、4回目にもとに戻ります。

σ₁₅ をさらに作用させると、もとに戻ります。

・Gal(ℚ(ζ)/ℚ(ζ^4))とGal(ℚ(ζ^4)/ℚ)のまとめ

4つ目、<σ₁₃>と<σ₁₅>で考えます。

Gal(ℚ(ζ)/ℚ(ζ⁴)) は、<σ₅> または <σ₁₃>。 この2つは位数4で逆回り。

Gal(ℚ(ζ⁴)/ℚ) は、<σ₇> または <σ₁₅>。 この2つは位数2で、ℚ(ζ⁴)に対する効果は同等。

ℚ(ζ)とℚ(ζ^4)の間にℚ(ζ^2)を加えて3段階の巡回を考える

これはうまく行っているのか自信はありません。

σ₉がζの偶数乗を固定することから、試してみます。

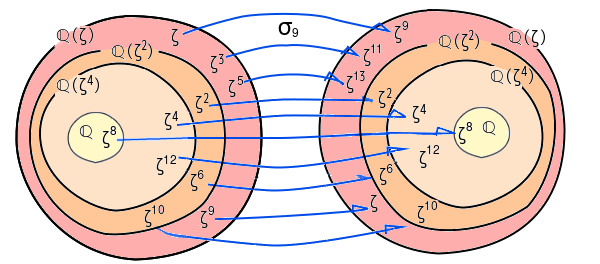
3段階になります。2段階に比べてℚ(ζ²)の部分が増えています。

・<σ9>と<σ3>による巡回の図示

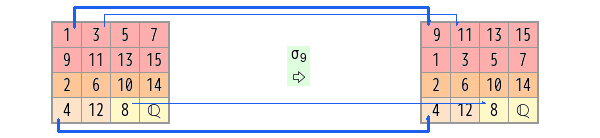
Gal(ℚ(ζ)/ℚ(ζ²)) は、<σ₉> で位数2の巡回をします。

⇩ σ₅ を作用させると、固定体であった部分が変換されます。

そこから σ₉を作用させると、ℚ(ζ²)の外側は、別の経路で巡回し、2回目にもとに戻ります。

⇩ σ₅ をさらに作用させると、ℚ(ζ²)の部分がもとに戻ります。ところが、ℚ(ζ²)の外側はもとには戻らず先に進みます。上のℚ(ζ⁴)/ℚの時にはこの部分ももとに戻りました。

⇩ σ₅ をさらに作用させると、ℚ(ζ²)の部分は2回目の巡回を始めます。ℚ(ζ²)の外側はさらに進んで行きますが、これが巡回の最後です。つまりℚ(ζ²)の外側は位数4で巡回します。

⇩ σ₅ をさらに作用させると、ℚ(ζ²)の外側の部分ももとに戻りますが、全体を眺めるとσ₉を施した列と合わせて2度づつ同じものが出てきてしまいます。

・<σ9>と<σ5>と<σ3>による3段階の累巡回の図示

Gal(ℚ(ζ⁴)/ℚ) は、<σ₃> で位数2の巡回をします。

上の立体図に似ていますが、σ₉とσ₅の部分が、上の立体図に相当します。