1の16乗根が作る拡大体

ℚ(ζ)/ℚとその拡大次数

x¹⁶-1=0 の解は ζ = cos(360˚/16)+isin(360˚/16) として、1,ζ,ζ²,ζ³,…,ζ¹⁵の16個です。

ℚ(ζ) の拡大次数を調べるために、ζのℚ上の最小多項式を求めます。

16次の円分多項式、Φ₁₆(x)=O は、1の原始16乗根だけが解になる式です。

根は ζ,ζ³,ζ⁵,ζ⁷,ζ⁹,…,ζ¹⁵ と2の倍数を除いたもので8個です。φ(16)=2³(2-1)=8 でも確認できます。

Φ₁₆(x)=O の最小分解体も ℚ(ζ) です。

ℚ(ζ)/ℚの自己同型写像

ℚ(ζ)のζⁱを別のζ^jに対応付ける写像のうち、1の原始16乗根に移すものだけを考えます。

具体的に計算してみます。ここでも、

σi(ζ)=ζi (i=1,3,5,7,…,15)

とします。σ₁は恒等変換です。

同時に、5乗根の時と同様に、同型写像の条件を満たすようにζ¹以外の移り先の組み合わせも確認します。

σの添字が偶数になる変換は有理数になってしまうものがあるので、同型写像になりません。

巡回群になっているか

さらに 自己同型写像 σ₁ 〜 σ₁₅ が巡回群になっているかを調べます。より正確に書くと、どれを生成元とすれば巡回群になるかということです。

結論から言うと、全体を巡回する生成元はありません

σ₃ σ₅ σ₁₁ σ₁₃ は位数4で、その他は位数2で巡回します。以下で見ていきます。

σ3を生成元とする巡回群

まずはσ₃を繰り返し作用させた表です。

ζ^kは初期値です。k=1から始めると、4回で1に戻ります。1からの巡回で出てこない5を初期値にすると別の値をとってやはり4回で戻ります。さらに出てこない2,4,10を初期値にすると、それぞれ別の経路で2回で戻ります。8で始めると変化しません。

2の倍数乗はσとしては出てきませんが、ζの2の倍数乗はℚ(ζ)には含まれますので、適切に移されなければなりません。2回で別の偶数乗に移されうまく行っています。8乗が変化しないのもζ⁸=-1で有理数だから適切です。

σ5を生成元とする巡回群

σ₃ の他に σ₅ も同様です。書籍Iのテキストでは、これを採用しています。累巡回拡大を作っています。

やはり、4回で1に戻ります。1からの巡回で出てこない3を初期値にすると別の値をとってやはり4回で戻ります。さらに出てこない2,6を初期値にすると、それぞれ別の経路で2回で戻ります。4,8,12で始めると変化しません。

その他4回で巡回するもの

σ₁₁ は σ₃ に、σ₁₃ は σ₅ に似ています。

2回で巡回するもの

σ₇,σ₉,σ₁₅ が最大2回で巡回します。変化しないものも混ざっています。

σ₇ は σ₁₅ に似ています。σ₉は偶数を固定しています。

σ5から累巡回拡大を考える

書籍Iのテキストに従い、σ₅を最初に考えます。

σ₅の巡回を再掲します。

1 5 9 13 1 はζの累乗指数であると同時に、σの添字でもあります。

{σ₅¹, σ₅², σ₅³, σ₅⁴=e} = {σ₅, σ₉, σ₁₃, e} = <σ₅> はGal(ℚ(ζ)/ℚ)の部分群になります。

<σ₅> に対応する固定体は、巡回の確認表から、ℚ(ζ⁴,ζ⁸,ζ¹²) = ℚ(ζ⁴) とわかります。

つまり、Gal(ℚ(ζ)/ℚ(ζ⁴)) = <σ₅> = {σ₅, σ₉, σ₁₃, e} です。

ℚ(ζ)/ℚ(ζ^4)の自己同型写像を図示

σ₅, σ₉, σ₁₃ の作用を図示します。

ℚ(ζ)のζⁱ (i=1,2,3,…,15) を入れ替えながら、ℚ(ζ⁴)を固定体にすることがわかります。

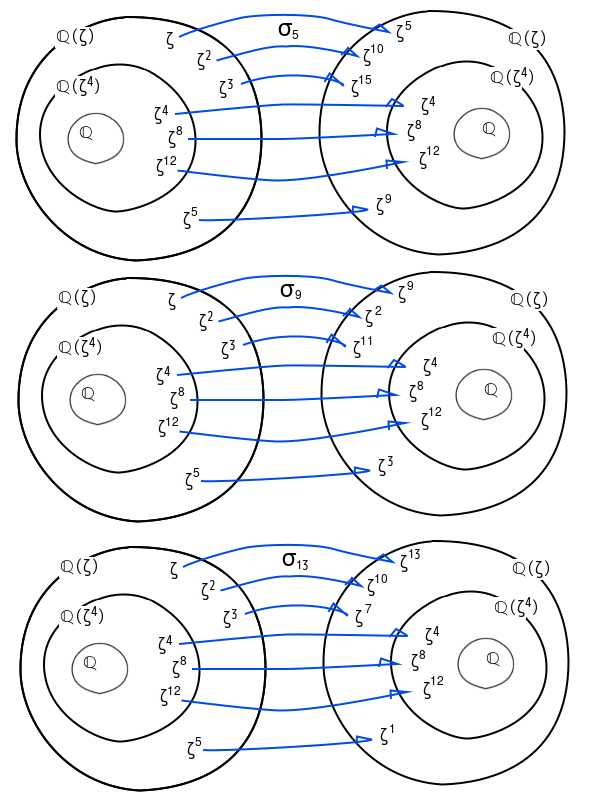
ℚ(ζ^4)/ℚ

次に、Gal(ℚ(ζ⁴)/ℚ) を考えます。ζ⁴を、ζ⁴,ζ⁸,ζ¹² のどれかに移す写像です。

σ_i(ζ)=ζⁱ (i=1,3,5,7,…,15)から探します。既に出てきた i=5,9,13 は当然不変にします。残る 3,7,11,15 はどれも同じ所に移します。

σj(ζ4)=ζ12
σj(ζ8)=ζ8
σj(ζ12)=ζ4  (j=3,7,11,15)

ζ⁴は虚数単位 i ですから、[ℚ(ζ⁴):ℚ] = 2 です。

巡回する様子を確認します。

k=3,7,11,15 のうちどれをとっても、この範囲では同じです。

8は不変です。これはζ⁸が-1と有理数だからです。したがって、ζ⁴とζ¹²が交換する以外に動かしようがありません。変換は恒等写像とあわせて2つだけということになります。

ちなみに、σ_j^sがなにに変化しているのかを見てみます。これはζ¹の変換先でわかります。

[ℚ(ζ⁴):ℚ] = 2 のことを考えると、位数2で巡回している7,15の方が都合が良さそうです。

ℚ(ζ⁴)への写像としては同等ですから、3,11でもいいのかもしれませんが、とりあえず、最初の7をとって、おきます。

Gal(ℚ(ζ4)/ℚ) = <σ7> = {e,σ7}

とできるでしょう。7×7=49=16×3+1=1 (mod16)です

ℚ(ζ^4)/ℚの自己同型写像を図示

ζ⁸は-1なので有理数の中にいます。実は、ζ⁴ = i 、ζ¹² = -i です。

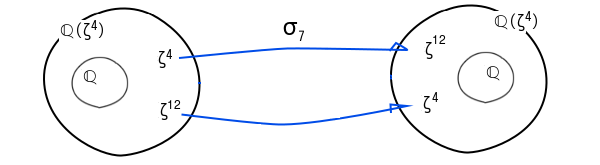
σ₇は、 ζ = cos(360˚/16)+isin(360˚/16) として σ₇(ζ)=ζ⁷ と定義されたものです。ℚ(ζ⁴)の中ではσ₃も、σ₁₁も、σ₁₅も同じ写像になります。

ℚ(ζ^4)を中間体とする累巡回拡大の吟味

Gal(ℚ(ζ)/ℚ)={σ₁=e,σ₃,σ₅,σ₇,σ₉,σ₁₁,σ₁₃,σ₁₅} です。

Gal(ℚ(ζ)/ℚ(ζ⁴)) = {e,σ₅,σ₉,σ₁₃} は巡回群になります。

Gal(ℚ(ζ⁴)/ℚ) = {e,σ₇} も巡回群です。

ℚ(ζ)/ℚ は、累巡回拡大ということができます。

{e,σ₇}と{e,σ₅,σ₉,σ₁₃}を組み合わせて、Gal(ℚ(ζ)/ℚ)の全部の元が出てくることを示すことができます。

σの添字は掛け算をして mod 16 します。

σ₁₅を採用しても同じです。

σ₇,σ₁₅ではなく、σ₃,σ₁₁を採用しても同じになりますが、<σ₃>と書くと巡回するのに4つの元を廻るので、気分が晴れません。

それは <σ₃>が{e,σ₃}ではなく、{e,σ₃,σ₉,σ₁₁}だからです。

ただ、ζ⁴等への作用は、eとσ₉で同じ、σ₃とσ₁₁で同じ、<σ₅>の組み合わせで出てくる写像も顔ぶれは同じです。

<σ₁₁>も似たようなものです。

σ5以外の選択肢はあるか

σ5から累巡回拡大を考えるでは書籍Iのテキストで採用されていたσ₅からはじめて累巡回拡大を考えました。他にやりかたはないのでしょうか。

σ₅で巡回の確認をした時にζ⁴、ζ¹²が変化していないことから、固定体を導き出せました。同様なことが、他の元からできないかを見てみます。

σ₃とσ₁₁も位数4で巡回しますが、ζ⁸以外に変化しないものがありません。

σ₁₃はσ₅と逆順で巡回し、ζ⁴、ζ¹²が変化しません。

σ₉はζのすべての偶数乗を固定します。

候補は、13と9です。

σ13から累巡回拡大を考える

σ₅同様に、ℚ(ζ⁴)を固定体にします。

次は ζ⁴を、ζ⁴,ζ⁸,ζ¹² のどれかに移す写像を探します。

やはり、σ_i(ζ)=ζⁱ (i=1,3,5,7,…,15)から探します。既に出てきた i=13,9,5 は当然不変にします。残る 3,7,11,15 はどれも同じ所に移します。

あとは、σ₅ の時と同様になります。

結論として、σ₁₃ から考えると

Gal(ℚ(ζ)/ℚ(ζ⁴)) = {e,σ₁₃,σ₉,σ₅} =<σ₁₃>は巡回群になります。

Gal(ℚ(ζ⁴)/ℚ) = {e,σ₇} =<σ₇>も巡回群です。

ℚ(ζ)/ℚ は、累巡回拡大ということができます。

巡回の順序が異なるだけで、群としては同じものになります。

ℚ(ζ^4)を中間体とする累巡回拡大の結論

Gal(ℚ(ζ)/ℚ(ζ4)) = <σ5> = {e, σ5, σ9, σ13}
Gal(ℚ(ζ4)/ℚ) = <σ7> = {e,σ7}

生成元は次の様にしても同等です。

Gal(ℚ(ζ)/ℚ(ζ4)) = <σ5> = {e, σ5, σ9, σ13}
Gal(ℚ(ζ4)/ℚ) = <σ15> = {e,σ15}

Gal(ℚ(ζ)/ℚ(ζ4)) = <σ13> = {e, σ13, σ9, σ5}
Gal(ℚ(ζ4)/ℚ) = <σ7> = {e,σ7}

Gal(ℚ(ζ)/ℚ(ζ4)) = <σ13> = {e, σ13, σ9, σ5}
Gal(ℚ(ζ4)/ℚ) = <σ15> = {e,σ15}

σ9から累巡回拡大を考える

σ₉の巡回を再掲します

σ₉は偶数乗を固定します。書籍Iのテキストの定義5.8のガロア拡大の定義では、

𝕂を𝔽の拡大体とし,ℂに含まれているものとする。𝕂に作用する𝔽の元を不変にする同型写像が, すべて自己同型写像になるとき, 「𝕂は𝔽のガロア拡大体である」, 「𝕂/𝔽はガロア拡大である」と表す。このときの自己同型群を𝕂の𝔽上のガロア群といい、Gal(𝕂/𝔽)で表す。

です。

この定義だと、「𝔽の元を不変にする同型写像」をすべて数え上げることができるか、確信が持てませんが、今回の話の流れでは、ℚ(ζ)における自己同型写像σ_iのうち、上記のようにζの偶数乗を固定するのはσ₉だけです。そして固定される群はℚ(ζ²)とわかります。

σ9(ζ) = ζ9
σ92(ζ) = σ9(ζ9) = (σ9(ζ))9 = ζ81 = ζ1 (mod 16)

なので、σ₉² = e ですから、巡回群になります。

Gal(ℚ(ζ)/ℚ(ζ²)) = <σ₉> = {e,σ₉} です。

σ9からの2つめはℚ(ζ^2)/ℚ

固定体はℚ(ζ²)なので、Gal(ℚ(ζ²)/ℚ) を考えることになります。

ζ²を、ζ²,…,ζ¹⁴ のどれかに移す写像です。

やはり、σ_i(ζ)=ζⁱ (i=1,3,5,7,…,15)から探します。i=1 と既に出てきた i=9 は当然不変で、移すことはありませんから除外です。

下の表はまとめて確認しているので無駄な部分も有ります。

ほとんど位数2で巡回してしまいますが4まで計算しています。

巡回ででてこなかったζ^jがσ_iによって、どこに移るかを調べ尽くしています。たとえば σ₃でいうと、2,6しか出てきませんから、4の移り先を調べ、10からの写り先を調べています。全部の偶数乗が出てきたら終わりです。8は-1で有理数なので除外しています。

結局、位数4の巡回はありません。巡回してζ²が、ζ²,…,ζ¹⁴ に移る群が作れないことを意味します。

σ₅とσ₁₃は固定される元が有ります。ζ⁴,ζ¹²です。それを除いて、巡回してζ²が、ζ²,ζ⁶,ζ¹⁰,ζ¹⁴に移るだけでもいいので少し期待が持てます。

σ₅とσ₁₃は、偶数の変換はまったく同じです。(ζ²)⁸=1 からσの添え字は mod 8 で同じになっている様子です。

ℚ(ζ²)の中でζ⁴,ζ¹²を固定するのはσ₅だけです(σ₁₃は同じものです)。

σ5(ζ2) = ζ10
σ52(ζ2) = σ5(σ5(ζ2)) = σ5(ζ10) = (σ5(ζ))10 = (ζ5)10 = ζ50 = ζ2 (mod 16)

なので、ℚ(ζ²)の世界では、σ₅² = e になり、巡回群になります。

ℚ(ζ)の世界では、σ₅² = σ₉ でしたから、ちょっと混乱します。これが正しいとすると、

Gal(ℚ(ζ²)/ℚ(ζ⁴)) = <σ₅> = {e,σ₅} です。

σ9からの3つめはℚ(ζ^4)/ℚ

ℚ(ζ²)/ℚのはずが、ℚ(ζ²)/ℚ(ζ⁴)となってしまったので、ℚ(ζ⁴)/ℚ です。

ζ⁴を、ζ⁴,ζ¹² のどちらかに移す写像です。

上の表で、σ₃, σ₇, σ₁₁, σ₁₅ がこれに当たります。添字を mod 4 で見れば同一なのでしょう。

σ3(ζ4) = ζ12
σ32(ζ4) = σ3(σ3(ζ4)) = σ3(ζ12) = (σ3(ζ))12 = (ζ3)12 = ζ36 = ζ4 (mod 16)

なので、ℚ(ζ⁴)の世界では、σ₃² = e になり、巡回群になります。

これもℚ(ζ)の世界では、σ₃² = σ₉ でしたから、ちょっと混乱します。これが正しいとすると、

Gal(ℚ(ζ⁴)/ℚ) = <σ₃> = {e,σ₃} です。

ℚ(ζ^2),ℚ(ζ^4)を中間体とする累巡回拡大の結論

ℚ(ζ)/ℚ は、このシナリオでも累巡回拡大ということができるのではないでしょうか。

Gal(ℚ(ζ)/ℚ(ζ2)) = <σ9> = {e,σ9}
Gal(ℚ(ζ2)/ℚ(ζ4)) = <σ5> = {e,σ5}
Gal(ℚ(ζ4)/ℚ) = <σ3> = {e,σ3}

このページでは一貫して、

ζ = cos(360˚/16)+isin(360˚/16)
σi(ζ)=ζi (i=1,3,5,7,…,15)

と定義されたものです。

ただし、ℚ(ζ²)の中にはζという元はありません。ですから、例えば、σ₅(ζ)=ζ⁵ という定義はℚ(ζ²)の中ではできないのですが、σ₅(ζ)=ζ⁵ という定義は σ₅(ζ²)=ζ¹⁰ と同じですから、問題ありません。

σ₉ は代わりがありませんが、σ₅はσ₁₃でも構いません。σ₃はσ₇, σ₁₁, σ₁₅ のどれかに代えてもかまいません。

9 - (5 or 13) - (3 or 7 or 11 or 15)

の組み合わせとなります。

もう一度変換の巡回を確認

もう一度σ_i^xがどの変換と同等になり、どのように巡回するのか、またどの元を固定するのかを確認して表にします。

σ₅からの考察では、<σ₅>あるいは<σ₁₃>と<σ₇>あるいは<σ₁₅>の組み合わせです。位数4で固定された元が2つある5あるいは13と、位数2で固定のない7あるいは15という組み合わせです。

σ₉からの考察では、<σ₉>と<σ₅>あるいは<σ₁₃>そして、<σ₃>あるいは<σ₇>あるいは<σ₁₁>あるいは<σ₁₅>の組み合わせです。位数2で固定された元が6つある9と、位数4で固定された元が2つあるものと、位数2または4で固定のないものとの組み合わせです。

固定される元があるかどうかは大いに手がかりとなりましたが、位数と固定の数はℚ(ζ)内で数えているので説得力はありません。

ℚ(ζ)/ℚのガロア群

Gal(ℚ(ζ)/ℚ)={σ₁=e,σ₃,σ₅,σ₇,σ₉,σ₁₁,σ₁₃,σ₁₅} と8個の元からなります。

σ₅からの考察で行き着いた

Gal(ℚ(ζ)/ℚ(ζ4)) = <σ5> = {e, σ5, σ9, σ13}
Gal(ℚ(ζ4)/ℚ) = <σ7> = {e,σ7}

から、この8個の元が過不足なく出てくることを示します。

計算は、σ₅とσ₇ならば 5×7=35≡3 (mod 16)などとなります。

σ₉からの考察で行き着いたのは

Gal(ℚ(ζ)/ℚ(ζ2)) = <σ9> = {e,σ9}
Gal(ℚ(ζ2)/ℚ(ζ4)) = <σ5> = {e,σ5}
Gal(ℚ(ζ4)/ℚ) = <σ3> = {e,σ3}

今度は3つの組み合わせなので、表の書き方を変えます。

計算は、σ₉とσ₅とσ₃ならば 9×5×3=135≡7 (mod 16)などとなります。

9 - (5 or 13) - (3 or 7 or 11 or 15) でしたから、9-13-7 も試してみます。