1の5乗根が作る拡大体

目次

ℚ(ζ)とその拡大次数

「f(x)=0の最小分解体に関する自己同型群をf(x)のガロア群という」(p.331)

厳密には言葉が足りないかもしれませんが、書籍Iのテキストにはこうあります。

x5-1=0 の解は ζ = cos72˚+isin72˚ として、1,ζ,ζ2,ζ3,ζ4の5つです。

x5-1=0 の最小分解体はℚ(ζ,ζ2,ζ3,ζ4)=ℚ(ζ)です。

拡大次数を調べるために、ζのℚ上の最小多項式を求めます。

円分多項式の議論から x4+x3+x2+x+1=0の根が ζ,ζ2,ζ3,ζ4 であり、拡大次数は4です。

|Gal(ℚ(ζ)/ℚ)| = [ℚ(ζ):ℚ] = 4

ガロア群 Gal(ℚ(ζ)/ℚ)

このガロア群の元は4つで、たとえば ζ を例に取れば ζをζ,ζ2,ζ3,ζ4に移す4つと考えられます。これを、

σi(ζ)=ζi (i=1,2,3,4)

とします。σiは恒等変換です。

ζの移り先しか示していませんが、これが決まれば、ζ2,ζ3,ζ4も自動的にきまって、このガロア群の元は4つになります。

もしも、決まらない場合には4×3×2=24通りの組み合わせがありえます。

たとえば、ある変換σで σ(ζ1)=ζ2, σ(ζ2)=ζ4, σ(ζ3)=ζ1, σ(ζ4)=ζ3 と変換されるのを、2 4 1 3 と書くことにした場合、24通りの変換は次の様になります。

1 2 3 4
1 2 4 3
1 3 2 4
1 3 4 2
1 4 2 3
1 4 3 2
2 1 3 4
2 1 4 3
2 3 1 4
2 3 4 1
2 4 1 3
2 4 3 1
3 1 2 4
3 1 4 2
3 2 1 4
3 2 4 1
3 4 1 2
3 4 2 1
4 1 2 3
4 1 3 2
4 2 1 3
4 2 3 1
4 3 1 2
4 3 2 1

写像としてはどれもありえますが、色付き以外は同型ではなく、したがってガロア群Gal(ℚ(ζ)/ℚ)の元による写像ではありません。

書籍Iのテキストでは、「同型写像 σi を、σi(ζ)=ζi と定める」と書くことで色付きの写像を選んだことにした上で、同型写像の移り先がℚ(ζ)の元なので自己同型だと言っているのです。ζの移る先が4つしかなくて、同型写像が4つあることがわかっているので、この4つは全部同型になっているものを選択できるはずだという論法です。

どうやって同型写像を選んだか

もう少し踏み込んで確認します。σ2(ζ)=ζ2 と定めた時に、ζ2 〜 ζ4 が何に移るかは6通りの組み合わせがあります。どれが同型写像の結果であるかは、次のように計算して求めます。

σ2(ζ2)=σ2(ζ・ζ)
      =σ2(ζ)・σ2(ζ)
      =ζ2・ζ2
      =ζ4

この計算で σ2(ζ・ζ)=σ2(ζ)・σ2(ζ) が、同型写像の条件である、

f(xy)=f(x)f(y)

が成立するように移り先を選び出しているのです。同様に

σ2(ζ3)=σ2(ζ・ζ・ζ)
      =σ2(ζ)・σ2(ζ)・σ2(ζ)
      =(σ2(ζ))3
      =(ζ2)3
      =ζ6
      =ζ
σ2(ζ4)=σ2(ζ・ζ・ζ・ζ)
      =σ2(ζ)・σ2(ζ)・σ2(ζ)・σ2(ζ)
      =(σ2(ζ))4
      =(ζ2)4
      =ζ8
      =ζ3

σ2による変換の結果を表にすると次のようになります。

σ2による変換
ζ1→ζ2
ζ2→ζ4
ζ3→ζ1
ζ4→ζ3

これを指数だけ書いて次の様に表すことにします。

σ2
12
24
31
43

24通り並べた時は横に並んでいましたが、ここでは縦に並べました。

4つの自己同型写像による変換の表

σi(ζ)=ζi (i=1,2,3,4) によるζ以外の元の移り先を指数だけで示した表です。σ1が恒等変換なので変換前のζの指数と同じです。

ζi の移り先
σ1σ2σ3σ4
11234
22413
33142
44321

Gal(ℚ(ζ)/ℚ)={σ1,σ2,σ3,σ4} です。

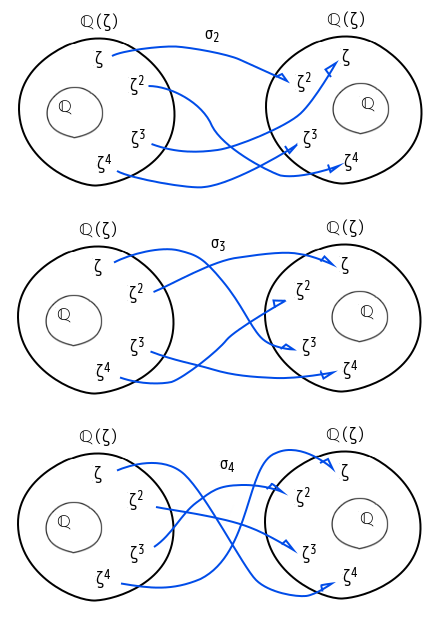
σiの写像のイメージ図です。σ1は恒等変換なので省きました。

いつもは、右側のζを矢印が水平になるように順番を変えています。すると上の表の順に対応します。今回はこっちのほうがイメージが湧きやすいかなと思って変えてみました。良かったのかちょっと迷っています。

巡回群になっているか

さらに σ1 〜 σ4 が巡回群になっているかが、次の注目点です。より正確に書くと、どれを生成元とすれば巡回群になるかということです。

まずはσ2を繰り返しζに作用させます

σ22(ζ)=(σ2σ2)(ζ)
      =σ2(σ2(ζ))
      =σ2(ζ2)
      =σ2(ζ)・σ2(ζ)
      =(σ2(ζ))2
      =(ζ2)2
      =ζ4
σ23(ζ)=σ2(σ22(ζ))
      =σ2(ζ4)
      =(σ2(ζ))4
      =(ζ2)4
      =ζ8
      =ζ3
σ24(ζ)=σ2(σ23(ζ))
      =σ2(ζ3)
      =(σ2(ζ))3
      =(ζ2)3
      =ζ6
      =ζ

つまりσ2を繰り返しζに作用させた場合、次の様に循環します。

ζ1σ2
→		 ζ2σ2
→		 ζ4σ2
→		 ζ3σ2
→		 ζ1

ζを変換した時の変換後の指数がσの添字になるという決め方でしたから、σ24(ζ)=ζ ということは、σ24=σ1 であることを意味します。

したがって、

σ21=σ2
σ22=σ4
σ23=σ3
σ24=σ1=e

σ2 は巡回群の生成元となります。

Gal(ℚ(ζ)/ℚ)={e,σ2,σ22,σ23}

生成元は一つだけか

σ2 だけでなく、σ3 も生成元となります。

次の表のσ2 の行では、ζ1 が、σ2 を作用させるたびにどうなるかをζの指数だけで書き出しています。一巡して4回目の作用で1に戻っています。

σ3 の行では逆順で巡回して1に戻ってきます。

σ4は2回目の作用で戻ってしまいます。2,3乗がでてきませんので、初期値を2とすると、やはり2回めで2に戻ります。全体を巡回しません。

巡回するかの確認
σi ζk σi1 σi2 σi3 σi4ζkは初期値
σ111111 元々恒等変換
σ212431 全体を巡回
σ313421 全体を巡回
σ4141 反転(2つを巡回)
σ4232

表計算計算式の紹介

移り先の確認

写像の移り先を計算するのは難しくはないのですが、間違えずに多数こなすのは面倒なので表計算ソフトを使うのが便利です。

LibreOfficeのCalcを使用しましたが、Excelでもできるはずです。

C3〜E5までが計算式になっています。ひとつのセルに計算式を入れて、後はコピーするだけでできます。

ζi の移り先
ABCDE
1 σ1σ2σ3σ4
2 ζ11234
3 ζ22413
4 ζ33142
5 ζ44321

C3の計算式は、「=MOD($B3*C$2,5)」B3×C2を5で割った余りを出します。

$がついているBと、2は別のセルにコピーされても位置を相対的に調整せず固定されます。この仕組みのおかげで、コピーすれば計算式は正しく設定されます。

ζi の移り先 表計算の計算式
ABCDE
1 σ1σ2σ3σ4
2 ζ11234
3 ζ22=MOD($B3*C$2,5)=MOD($B3*D$2,5)=MOD($B3*E$2,5)
4 ζ33=MOD($B4*C$2,5)=MOD($B4*D$2,5)=MOD($B4*E$2,5)
5 ζ44=MOD($B5*C$2,5)=MOD($B5*D$2,5)=MOD($B5*E$2,5)

巡回の確認

上の「生成元は一つだけか」に書いた表にB列を追加しています。σiのiです。計算式をコピーで設定できるようにとの追加です。

D2〜G7までが計算式になっています。ひとつのセルに計算式を入れて、後はコピーするだけでできます。

巡回するかの確認
AB CDEFG
1 σi i ζk σi1 σi2 σi3 σi4ζkは初期値
2σ11 11111 元々恒等変換
3σ22 12431 全体を巡回
4σ22 24312 当然2から始めても全体を巡回
5σ33 13421 全体を巡回
6σ44 14141 反転(2つを巡回)
7σ44 23232

D2の計算式は、「=MOD(C2*$B2,5))」C2×B2を5で割った余りを出します。

D2に書かれたC2は一つ左のセルの値という意味です。$B2はB列の同じ行という意味です。

$がついているBは別のセルにコピーされても位置を相対的に調整せず固定されます。この仕組みのおかげで、コピーすれば計算式は正しく設定されます。

途中で巡回が終わっている場合は目視で判断する必要があります。

巡回するかの確認
AB CDEFG
1 σi i ζk σi1 σi2 σi3 σi4ζkは初期値
2σ11 1=MOD(C2*$B2,5))=MOD(D2*$B2,5))=MOD(E2*$B2,5))=MOD(F2*$B2,5)) 元々恒等変換
3σ22 1=MOD(C3*$B3,5))=MOD(D3*$B3,5))=MOD(E3*$B3,5))=MOD(F3*$B3,5)) 全体を巡回
4σ22 2=MOD(C4*$B4,5))=MOD(D4*$B4,5))=MOD(E4*$B4,5))=MOD(F4*$B4,5)) 当然2から始めても全体を巡回
5σ33 1=MOD(C5*$B5,5))=MOD(D5*$B5,5))=MOD(E5*$B5,5))=MOD(F5*$B5,5)) 全体を巡回
6σ44 1=MOD(C6*$B6,5))=MOD(D6*$B6,5))=MOD(E6*$B6,5))=MOD(F6*$B6,5)) 反転(2つを巡回)
7σ44 2=MOD(C7*$B7,5))=MOD(D7*$B7,5))=MOD(E7*$B7,5))=MOD(f7*$B7,5))

このページに使用した特殊な記号

角度を表すdegreeに使いました。U+00B0の方は全角扱い(日本語-日本のロケールのせいだと思いますが)になるので、U+02DAを使っています

˚ U+02DA RING ABOVE

° U+00B0 DEGREE SIGN